Dopo aver spiegato nei mesi scorsi il funzionamento dell’indice SICS, grazie alla collaborazione di Fabio Fin, esperto di match analysis e laureando in Scienze Statistiche all’Università degli Studi di Napoli ‘Federico II’, introduciamo oggi uno strumento che deriva dal mondo anglosassone e sta conoscendo un crescente interesse.
Gli appassionati e i tecnici sportivi più attenti avranno certamente sentito parlare di Expected Goals, indici statistici applicati al calcio, che negli ultimi mesi hanno avuto diffusione anche nel panorama sportivo italiano.
L’indice Expected Goals (sigla xG) nasce negli USA e viene usato anche per l’hockey. Si diffonde nel Regno Unito ed ha un successo crescente.
Un indice statistico è una combinazione matematica di più valori che restituisce un unico risultato di sintesi in modo da ridurre la complessità e la vastezza dei dati.
In particolare, gli Expected Goals, tradotti in italiano come Gol Attesi, richiamano i cosiddetti Expected values (o valori attesi), cioè i valori medi di una variabile casuale.
La variabile casuale è un carattere che può assumere uno di più valori (di supporto) in relazione al fenomeno di studio dall’esito incerto. Gli esempi più comuni di variabile casuale sono il lancio di una moneta (due esiti, testa o croce, entrambi con una probabilità del 50%) o il lancio di un dado (sei facce con stessa probabilità se il dado non è truccato). In modo simile, anche il numero di tiri o gol è incerto.
Allora, il valore atteso è dato dalla somma dei possibili esiti, ciascuno pesato per la probabilità che esso si realizzi. (Se il supporto non è discreto, cioè finito o numerabile, ma continuo, si utilizza il calcolo integrale che è pur sempre una somma).
Gli Expected Goals, dunque, sono una combinazione lineare dei tiri pesati con coefficienti ponderali che fornisce la misura media del numero di gol per l’incontro analizzato. Sono indicate, allora, quante reti avrebbe dovuto segnare una squadra sulla base di quanto costruito sul campo.
Nel loro calcolo, occorre rilevare ogni tiro e associarlo al peso specifico, cioè il suo tasso di conversione storico, ovvero: un altro indice statistico che varia tra 0 e 1, come una probabilità, definendo quindi la percentuale di conversione del tiro in gol. In tal senso, è necessario distinguere i tiri sulla base di categorie di appartenenza. Gli attributi usualmente utilizzati sono la posizione di tiro, le tipologie di tiro e di azione offensiva e la pressione difensiva.
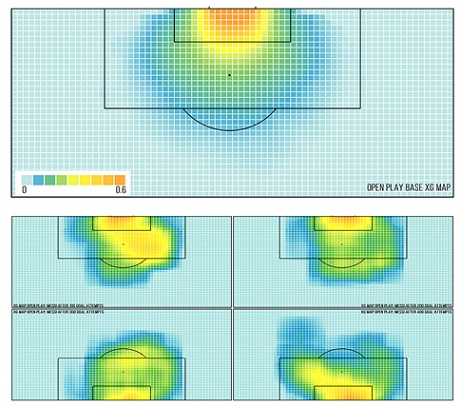
Nel dettaglio, per la posizione si usufruisce di una mappa di allocazione che suddivide la metà campo di gioco in più celle, ciascuna associata ad un tasso. Aumentando il numero di variabili si possono ottenere mappe più specifiche, ad esempio quella dei calci d’angolo o dei tiri da fermo. In tal senso, in Figura sono illustrate le mappe realizzate dal sito Scisport secondo le specificazioni citate. Taluni autori chiamano questo tasso xG locale, differenziandolo dall’xG globale che corrisponde agli Expected Goals di gara.
E’ importante poi considerare l’organizzazione difensiva di una squadra, infatti, meglio si difendono gli avversari più è difficile segnare. E’ però impossibile quantificare direttamente la pressione difensiva, per cui si ricorre a variabili latenti, cioè proxy.
Una strategia consiste nell’esaminare i diversi stati di gioco, cioè i differenziali nel punteggio, occorsi durante una gara. Infatti, in caso di vantaggio si ha interesse nel non alterare il risultato, assumendo una buona organizzazione difensiva, viceversa compromessa durante una situazione di svantaggio, quando aumenta la spinta offensiva.
E’ compito dell’autore, in base ai dati a disposizione e alla bontà dei risultati, discernere tra i fattori di correzione che caratterizzano i tassi di conversione, che nella loro versione elementare sono dati dal solo rapporto tra numero di gol e numero di tiri, mentre in quella più complessa considerano anche le capacità balistiche del singolo calciatore.
Ad esempio, Nainggolan è più bravo della media da fuori area, Callejon nell’inserimento sulla destra.
Dal punto di vista computazionale, gli analisti annotano i tiri in serie storiche, cioè per l’arco di più campionati passati, in relazione alle categorie considerate. Come avviene per i valori attesi, è giusto accompagnare le stime degli Expected Goals con misure della loro variabilità, cioè la varianza o la deviazione standard (sua radice quadrata).
In definitiva, gli Expected Goals sono una misura dell’efficacia offensiva di una squadra, che tiene conto non più della sola quantità di tiri, ma anche della loro qualità. I Gol Attesi sono utilizzati in modo alternativo ai gol reali per fare analisi sulle prestazioni. Sono spesso fatti confronti tra le differenze reti reali e attese per valutare l’andamento di una competizione. Inoltre, possono essere calcolati gli Expected Goals del singolo atleta, quali indicatori della sua capacità realizzativa. Per un finalizzatore è opportuno che lo scarto tra gol reali e attesi sia minimo, mentre per un fantasista può essere più ampio, in quanto lo si giudica secondo diversi parametri, come il numero di occasioni create.
Gli Expected Goals, come qualsivoglia variabile di gioco, possono essere inseriti in ulteriori applicazioni statistiche di analisi multivariata e modellistica. A tal proposito, un modello statistico consta nel relazionare una variabile di risposta con una o più variabili dipendenti al fine di verificare se sussista una incidenza delle seconde sulla prima e in caso affermativo quantificarla. Come in economia si esamina quanto possa guadagnare un lavoratore (risposta) in base alle proprie caratteristiche (dipendenti), nel calcio si può studiare l’impatto degli Expected Goals (dipendente) sui punti in classifica (risposta). E’ ridondante un modello che relaziona gol reali e Gol Attesi, poiché gli stessi modelli forniscono una stima delle aspettative medie, nota come regressione. Può essere adoperato invece il loro indice di correlazione, stante il calcolo delle varianze, per misurare quanto variano assieme.
Secondo un diverso approccio, sarebbe interessante adoperare gli Expected Goals in modelli previsionali in serie storiche, come avviene per le predizione sulle variabili macroeconomiche. D’altro canto, i gol reali potrebbero essere una risposta in un modello per variabili discrete, per superare la logica dell’arrotondamento tipica degli Expected Goals.
Si legge che una squadra ha creato, per esempio, 1.4 Gol Attesi ma, invero, non è possibile segnare 1.4 gol. Ad ogni modo, il loro impiego in modelli è tuttora raro, mentre è doveroso specificare che inserirli in un modello non fa di loro un modello, ma, ovviamente un indice inserito in un modello.
In conclusione: il calcio è uno sport complesso, il cui esito degli incontri non sempre esplica al meglio quanto svoltosi sul terreno di gioco, dunque, gli strumenti statistici sono opportuni per indagare gli eventi casuali che lo caratterizzano.